Innleiingsdel
I    -  Tonalitetsspørsmålet i etnomusikologien

II   -  Om musikknotasjonen
III  -  Musikkmiljøet på Nordmøre
IV   -  Magnhild Havdal Almhjell og opptaka etter henne
V    -  Statistisk behandling av materialet
VI   -  Tonal gravitasjon
VII  -  Melodisk analyse
VIII -  Konklusjon
IX   -  Notar og kjeldor

VI — Tonal gravitasjon

Kva er gravitasjon?

Gravitasjon kan svært grovt seiast å vera eit uttrykk for tiltrekning mellom ulike legeme av ein relativ styrke som står i forhold til massen i kvart legeme og avstanden mellom dei. Eit tungt legeme som jorda øver dermed ei netto tiltrekning på eit lett legeme som eit eple, og eplet «dett ‘ned’» mot jorda.

To legeme som er kommer for langt inn i kvarandre sine gravitasjonsfelt vil falle saman, enten med at eit lett legeme nærmar seg og fell saman med eit større (slik ein ser det med eplet og jorda) eller med at to legeme med relativt lik masse fell mot kvarandre. Tunge legeme har eit kraftigare og større gravitasjonsfelt enn lette legeme, og det kritiske punktet finst dermed lengre unna dei tunge legema enn dei lette. Eit legeme som er nær nok eit tyngre legeme til å bli gjort avhengig av det, men utan å vera nær nok til å falle saman med det, vil gå inn i eit «fall» parallelt med det tunge legemet, eller, med andre ord, gå inn i ein bane rundt det.

I vårt solsystem finst det større og mindre legeme som øver meir eller mindre tiltrekning på kvarandre. Såleis er sola det tyngste legemet, og dermed det legemet ein kan kalle sentrum. Rundt dette sentret går så planetane. Ein del mindre legeme er så små at dei blir utsette for større relativ tiltrekning frå éin av planetane enn frå sola, slik at dei går inn i ein bane rundt denne planeten. Desse legema er det vi kallar månar.

Lokalt på ein planet er gravitasjonskreftene i alt vesentleg identiske med det vi kallar tyngdekrafta. ‘Opp’ og ‘ned’ — begrep som i prinsippet gir retninga i forhold til tyngdekrafta — er ikkje berre velkjente, men absolutt grunnleggande i vårt verdsbilde.

Gravitasjonseffektar og estetikk

Eg tek absolutt ikkje stilling til idear om «sfæranes harmoni» og liknande — dette er spørsmål som passar dårleg inn i ein moderne, vitskapleg samanheng.

Det eg hevdar, er at gravitasjonsbevisstheita er ein grunnleggande del av vår bevisstheit og eit av dei mest grunnleggande estetiske prinsippa. Menneska har ein tendens til å sortere inntrykk etter parameter som tungt og lett, sterkt og svakt. Bildekunstnarar og arkitektar reknar for eksempel mørke fargar for tyngre enn lyse fargar; musikarar kallar tonar med fleire svingningar i sekundet ‘høge’, i motsetning til ‘låge’ tonar med færre svingningar i sekundet. Musikarar deler i musikken i takter, der det første slaget (eller eit anna slag i nokre typar musikk) blir definert som tyngre enn dei andre.

På grunn av at gravitasjonsprinsippet i så stor grad ligg under vår persepsjon, er det rimeleg å tru at:

1) Gravitasjonsprinsippet kan vera eit nyttig utgangspunkt for ein analyse av eit musikalsk system.
2) Gravitasjonsprinsippet er intuitivt lett forståeleg, og kan brukast til å forklara tonale mekanismar åt folk med relativt lite kunnskapar om musikkteori.

Serleg ut frå punkt 2, er det lett å tenkje at dette må vera uvitskapleg, etter som folk med manglande musikkteoretisk bakgrunn så lett kan forstå prinsippa. Men om ein aksepterer den eksoteriske tanken om at enklast er best, så burde ikkje dette vera noko problem.

Gravitasjonsprinsippet i musikken

Vekt

Min hypotese er at kvart trinn i eit tonalt system kan formulerast å ha ei spesifikk «vekt». Denne vekta er ekvivalent med summen av alle rollar trinnet spelar i ulike kognitive, «grammatiske» strukturar innanfor systemet (eller systema). Ei trinn som kan beskrivast som

A) femte trinn i skalaen,
B) kvinten i tonikaakkorden,
C) grunntonen i dominantakkorden,
D) tersen i tonikaparallell

er altså tyngre enn eit trinn som berre kan beskrivast som

A) tersen i vekseldominanten
B) ledetone til dominanten.

På same måte er eit trinn som kan beskrivast som

A) første trinn i skalaen
B) finalis
C) skalaeige pentatont trinn

tyngre enn eit trinn som berre kan beskrivast som

A) den skalaeksterne naboen rett ovom femtetrinnet.

Konsekvensar


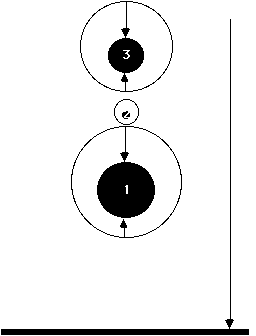
I skissa av gravitasjonsforhold vart det nemnt at legema har kritiske avstandar der legeme som kjem innafor vil gå mot overflata på dei, og at denne avstanden ligg lengre frå overflata di større massen av legemet er. Ei direkte overføring av dette prinsippet til musikken skulle medføre at ein hadde minimumsavstandar mellom ulike trinn, og at trongare avstandar enn desse skulle føre til samanfall. Vidare skulle dei tyngste trinna ha ein større «gravitasjonssone» enn dei lettaste. I praksis betyr dette at ein kan få ei slags «minste mulege avstand» ved t.d. første og femte trinn. I praksis blir må ein her ha med ein variabel til — generell nedovergåande gravitasjon. Denne er eit uttrykk for at det er lettare å gli ein halvtone ned til eit tungt trinn enn å gli ein halvtone opp. Dermed får vi eit noko modifisert bilde: Over eit tungt objekt får vi tiltrekningskrafta til dette objektet addert med den generelle nedovergåande krafta. I sum får vi altså ei forsterking av gravitasjonsfeltet, og det kritiske punktet flyttar seg oppover. Under objektet får vi derimot tiltrekningskrafta til objektet minus den generelle nedovergåande krafta. Vi får altså ei svekking av gravitasjonsfeltet, og det kritiske punktet kjem nærmare objektet. (Sjå teikninga.) I tradisjonell / moderne européisk tonalitet har vi t.d. eit kritisk punkt ved en halvtone under grunntonen, mens vi over grunntonen har eit kritisk punkt ved heiltonetrinnet. Kjem vi ned på ein liten sekund over grunntonen, forskyver vi tonaliteten, og den tidlegare grunntonen blir dominantisert.

I visse situasjonar, der eit marginalt trinn ligg på det kritiske punktet åt ein tyngre tone, får vi gjerne ei sterk melodisk binding mellom dei to, slik at ein ikkje kan gå til det lette trinnet utan å gå om det tunge.

Ved eit melodisk–harmonisk system vil vi få ei større eller mindre utjamning av effektane av den tonale gravitasjonen, ettersom dei melodiske og dei harmoniske kreftene ofte går motsett veg. Mens ein høg ledetone i eit melodisk system blir trekt mot grunntonen (og gjerne kompanserer for det med ein noko senka intonasjon), har ein i eit melodisk–harmonisk system gjerne den same dragninga mot grunntonen, men i tillegg ei tilsvarande, harmonisk dragning mot sentrum av (dominant-)akkorden, og intonasjonen av ledetonen er dermed frigjort i forhold til det kritiske punktet.

Universelt eller systemspesifikt?

Systemet i seg sjølv er ikkje, slik eg foreløpig ser det, stilspesifikt, men ein spesifikk stil med sine lokale eigenskapar vil føre til lokale virkningar ut ifrå universelle prinsipp. I stilar med utprega egaliserte trinn vil ein òg få egalisert behandling av trinna. I stilar med utprega ulik vekting av trinn vil ein få ulik behandling av dei.
Nærmast ein vektlaus (eller entropisk) tilstand får ein i streng tolvtonestil, der kvart trinn i prinsippet spelar same rolle, nemleg som éin av dei tolv. Heilt i den andre enden av skalaen finn vi den strengt pentatont oppbygde musikken med eit skarpt skilje mellom dei fem meir eller mindre tunge rammetonane og dei to utprega lette pien-tonane (utfyllingstonane).

Logisk / terminologisk oppbyggjing

Strukturen i denne delen

Dette delkapitlet er oppbygd av definisjonar og påstandar og har som mål å vise den logiske komposisjonen av analysemetoden i si foreløpige utgåve. Under nokre av definisjonane er det tillagt spesifikasjonar eller eksempel.
Eg må presisere at dette delkapitlet bør, serleg om det blir lese uavhengig av (eller føre) resten av avhandlinga, lesast strengt i rekkefølgje, ettersom kvar definisjon i prinsippet byggjer på dei føregåande definisjonane.

Definisjon 1 — trinn

Eg definerer eit trinn som eit frekvensområde av større eller mindre bandbreidd med stor sannsynleg tettheit av enkelttonar og som kan skiljast ut frå nabotrinn med eit mellomliggande frekvensområde med liten sannsynleg tettheit av enkelttonar.
 

Definisjon 2 — skalatrinn

Skalatrinn er det utvalet av trinn som utgjer ein skala. I praksis vil ein kunna bruke termen ‘trinn’ i staden.

Definisjon 3 — trinnvariant

Trinnvariant er termen for standardiserte variantar av skalatrinna.
 

Definisjon 4 — ambitus

Ambitus definerer eg som området mellom høgaste og lågaste trinn. Eg definerer ambitus i samband med slag, frasar, melodiar og melodigruppor.
 

Definisjon 5 — objekt

Eit objekt kan vera ein tone, eit trinn, ein melisme, ein ambitus eller summen av slike objekt i eit slag, ein frase eller ein melodi.

Definisjon 6 — masse = mental masse = tyngd

Mental masse definerer eg som den tenkte relative rollen det aktuelle objektet spelar i det aktuelle systemet hos komponisten og/eller utøvaren.

Påstand 1

Eit trinn med stor masse vil vera mykje bruka i det aktuelle systemet.
 

Definisjon 7 — massegivande faktor

Ein massegivande faktor er ein faktor som gir masse til det eller dei objekta han gjeld for.
 

Definisjon 8 — gravitasjon

Gravitasjon definerer eg som den tenkte relative tiltrekningskrafta mellom objekta.

Definisjon 9 — tiltrekkjing

Tiltrekkjing tilsvarar det konkrete utslaget av gravitasjon mellom to spesifikke objekt.

Påstand 2

Botnpunktet av songstemmen må reknast som eit objekt.
 

Definisjon 10 — gravitasjonsfelt

Eit gravitasjonsfelt definerer eg som det området kring eit objekt (f.eks. trinn) som blir dominert av gravitasjonen frå dette objektet.

Påstand 3

Massen av eit trinn bestemmer størrelsen på gravitasjonsfeltet.

Påstand 4

Den minimale avstanden mellom objekta er avhengig av størrelsen på gravitasjonsfelta deira.

Definisjon 11 — kritisk punkt

Det kritiske punktet er den minimale avstanden ein kan ha mellom to objekt (f.eks. trinn) utan at dei blir ustabile eller fell saman.

Definisjon 12 — pien-tone

Ein pien-tone er eit lett trinn som er oppbunde i si innføring og eventuelt vidareføring på ein måte som følgjer av gravitasjonskreftene frå dei to nabotrinna.
 

Definisjon 13 — melodisk tonesystem

Eit system der einstemmige melodiske bevegelsar utgjer basis for tonaliteten.
 

Påstand 5

I eit reint melodisk system vil gravitasjonsfelta kring dei tyngste trinna i stor grad vera eintydige.

Definisjon 13 — harmonisk tonesystem

Eit system der samklangar utgjer basis for tonaliteten.

Definisjon 14 — melodisk-harmonisk tonesystem

Eit system der melodiske bevegelsar og samklangar tilsaman utgjer basis for tonaliteten.
 

Påstand 6

I eit melodisk–harmonisk tonesystem vil gravitasjonsfelta kring kvart melodiske trinn balansere med gravitasjonsfelta i samband med det harmoniske fundamentet.
 

Vurdering av statistikken med bakgrunn i teorien om tonal gravitasjon

Med bakgrunn i den statistiske granskinga, teorien om tonal gravitasjon og dei momenta som er framkomne i del VI, vil eg no i korte trekk behandle dei tre kategoriane frå Magnhild-materialet på nytt.

Eit modalt, pentatont basert system

I det mørke mollmaterialet er det nokre tydelege trekk: T2 og T6 er i signifikant grad underrepresenterte. Og om vi no ser på dur-materialet, så er det der ein rett nok mindre tydeleg tendens til underrepresentasjon av T4 og T7. Om vi no tersforskyver desse toneartane, så viser det seg at vi får ein høg grad av konvergens:

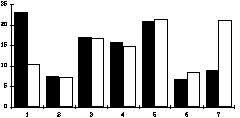
Mørk moll er her dei svarte søylane, og dur dei kvite. Verdiane for dur er her flytta ein ters, slik at 1 tilsvarar T1 i mørk moll og T6 i dur osv. Men stadig er det markert divergens i to tilfelle: Ved søylepara 1 og 7.
Likevel er dette oppløftande, og om vi no tolkar kategorien mørk moll som hovudsakleg eolisk, heretter kalt moll som ein samleterm for eolisk og det sporadiske frygiske og kategorien lys moll med sin høge sekst som hovudsakleg dorisk, kan vi sette opp eit modalt system som ser slik ut:
 

a h c d e f g a h c d
dorisk 1 2 3 4 5 6 7 1
dur 1 2 3 4 5 6 7 1
moll 1 2 3 4 5 6 7 1

I mange av visone i moll er mykje av melodikken basert på denne skalaen:

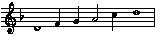
Om ein no reknar dei trinna som ikkje er representerte i denne skalaen som pien-notar og reknar med at desse notane har fast plassering i det modale systemet, får ein denne modifiserte utgåva av tabellen:
 

a (h) c d e (f) g a (h) c d
dorisk 1 2 (3) 4 5 (6) 7 1
dur 1 2 3 (4) 5 6 (7) 1
moll 1 (2) 3 4 5 (6) 7 1

Om vi no ser på dur, så skulle ein her etter teorien ha pien-tonane T4 og T7. I likheit med kva vi såg for eolisk, så stemmer dette bra, i og med at desse to trinna faktisk er dei minst brukte i denne kategorien. Da er neste spørsmål korleis dette stemmer for dorisk. Her er skal dei to pien-tonane vera T3 og T6.Dette stemmer svært bra når ein ser på T6 innanfor dorisk. Dette trinnet er det definitivt minst brukte. Men nest minst er forekomsten av T7. Her er det med andre ord noko som ikkje heilt stemmer. T3, som etter teorien ikkje skulle høre til den pentatone skalaen, er ikkje spesielt lite bruka — snarare tvert imot: Trinnet har ein forekomst på nærmare 17 prosent!
Med andre ord kan ikkje tilhørigheit til pentatonikken åleine gi trinna vekt. Ettersom trinnet er mykje bruka, følgjer det av min påstand 1 og definisjon 6 og 7 (sjå del V)  at ein eller fleire andre massegivande faktorar spelar inn.
Vi såg tidlegare at prosentdelen sprangvis innføring av dei ulike trinna danna eit interessant mønster i samband med dur og moll: T1, T3, T5 og T7 vart sprangvis innførte markant oftare enn dei andre trinna. Som eg nemnte i del VI, så hevdar Curt Sachs at tersoppbyggjing av tonaliteten er typisk for store deler av Europa. Om vi legg inn denne variabelen, så vil ein i dorisk få ein situasjon der T2 og T4 får større vekt på grunn av at dei er pentatont skalaeigne, mens T3, som ikkje er pentatont skalaeigen, får omtrent like mykje større vekt ut ifrå tersstrukturen. Resultatet vil da bli nettopp ei relativt jamn fordeling av T2, T3 og T4 i dorisk. I jonisk og eolisk, der tersstrukturen og dei pentatont skalaeigne tonane stort sett stemmer overeins, vil samanfalla føre til ei markant auke i vekta. Men både dur- og mollpentatonikken har ein tone i området grunntone–kvint som fell utanom: T2 i dur og T4 i moll. Vi ser da at forekomsten av desse er noko lågare enn ved T1, T3 og T5 i begge tilfella, noko som altså er lett forklarleg ut ifrå ei kvantifisering av dei massegivande faktorane for kvart trinn.

Pien-tonen i gravitasjonssamanheng

Vi såg i statistikk-kapitlet at kategoriane mørk og lys moll hadde ulik behandling av T6: Dorisk hadde mulegheiter for innføring både ovanfrå og nedanfrå, i motsetning til mørk moll, som så og seie utelukkande hadde innføring frå undersekunden eller ved tonegjentaking. Vurdert i samband med tonal gravitasjon er dette ei enkel nøtt: T6 står mellom eit relativt lett T7 og eit svært tungt T5. Når den i seg sjølv lette T6 ligg midt imellom eller nærmare T5, vil han bli dregen mot 5. trinnet, mens eit T6 tett oppunder T7 vil vera i likevekt og ha ei friare innføring.
I samband med det frygiske materialet (to av melodiane i gruppa moll eller mørk moll), er det særleg å merke seg at T2, som elles blir behandla relativt fritt, blir oppbunde til T1 i større grad enn det er tilfelle i eolisk.
Ei liknande behandling som den T6 i eolisk og frygisk får, får i nokon grad òg 3. trinnet i dorisk. Her er det spesielt verd å merke seg melodien «Guds Godhed ville vi prise».

Eit forsøk på talbasert bruk av prinsippa i tonal gravitasjon på materialet

Sjølv om eg ikkje har utvikla nokon presis matematisk metode for gravitasjonsorientert tonal analyse, vil eg avslutningsvis sette opp eit eksempel på korleis ein med å vekte dei ulike  massegivande faktorane kan utføre ein omtrentleg rekonstruksjon av trinnfordelinga i alle dei tre undersøkte kategoriane i ein felles modell. Dette har eg gjort på følgjande vis:
 
I EININGAR: 1 2 3 4 5 6 7 SUM
Dur 15,4 15,1 17,8 8,5 18,0 10,3 6,0 91,0
Dorisk 12,9 17,6 12,5 14,8 17,0 5,0 11,3 91,0
Moll 18,3 7,0 17,8 13,8 18,0 5,0 11,3 91,0
I PROSENT:
Dur 16,9 16,6 19,5 9,3 19,8 11,3 6,6 100,0
Dorisk 14,1 19,4 13,7 16,2 18,7 5,5 12,4 100,0
Moll 20,1 7,7 19,5 15,1 19,8 5,5 12,4 100,0

I grafisk form blir korrespondansen mellom det målte resultatet og den rekonstruerte tonaliteten slik, med den rekonstruerte tonaliteten merka med lyse punkt:

Moll

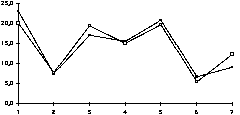
Dorisk


 

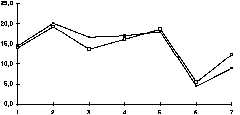
Dur

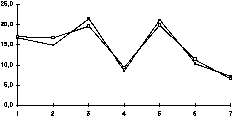
Kvart moment som er bruka som grunnlag for tildeling av einingar er basert på ei vurdering av kva tonale moment som på basis av mine kunnskapar om musikken etter Magnhild er vesentlege. Den spesifikke innsettinga av verdiar er subjektiv i den forstand at talverdiane ikkje kan isolerast som sjølvstendige observasjonsresultat i forkant av den talbaserte bruken av prinsippa.

Talverdiane har eg komme fram til med prøving og feiling: Med å variere tildelte verdiar etter dei ulike tonale momenta, såg eg kva virkning dei hadde for dei tre tonalitetstypane. Eg var her så og seie i dialog med materialet. Observasjonsdata fanst. Teorien fanst, og dei tonale momenta som rekna som viktige fanst. Oppgåva var å finne ut om teorien gjennom ei vekting av kvart tonalt element kunne vise samsvar med den variasjonen som allereie er påvist mellom dei ulike modi. Mulegheit til på dette viset å få høg grad av konvergens i alle tre kategoriar var meir eller mindre avhengig av at melodiane statistisk sett stort sett følgjer felles prinsipp, og at eg i vektinga av elementa kunne følgje dei same prinsippa.

Korleis ser så resultatet ut? Vi ser at mollkategorien stort sett viser høg grad av konvergens. Dei største avvika finn vi ved T3 og T7, men avvika er ikkje større enn at den relative vektinga mellom trinna grovt sett stemmer mellom observerte verdiar og berekna verdiar. I den doriske kategorien ser vi det same. Igjen er det dei same trinna som viser eit visst avvik, men ikkje meir enn at den relative vektinga grovt sett stemmer. I dur finn vi det største avviket ved T2 og T3. Heller ikkje her er avviket større enn at den relative vektinga grovt sett stemmer.

Det er med andre ord ikkje hundre prosent samsvar, men eit avvik opp til 4–5 prosentpoeng på enkelte verdiar er ikkje meir enn ein må rekne med.

Konklusjonen er at ein har ein så høg grad av konvergens at relevansen av teorien må kunna reknast som vesentleg.
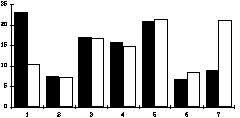
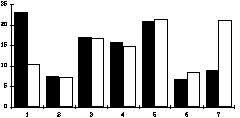